La influencia del tamaño de malla en la concentración de esfuerzos en un eje cilíndrico con filete de hombro bajo carga de tensión.
Por Juan Manuel Rodríguez (I.M., Ph.D.)
Confundador de Simulmax Engineering.
El objetivo de este artículo es ilustrar el efecto del tamaño de la malla en la predicción de la concentración de los esfuerzos mecánicos a través de simulaciones computacionales. Se realizó un análisis elástico lineal de la concentración de esfuerzo en un eje cilíndrico con filete de hombro en carga de tensión.
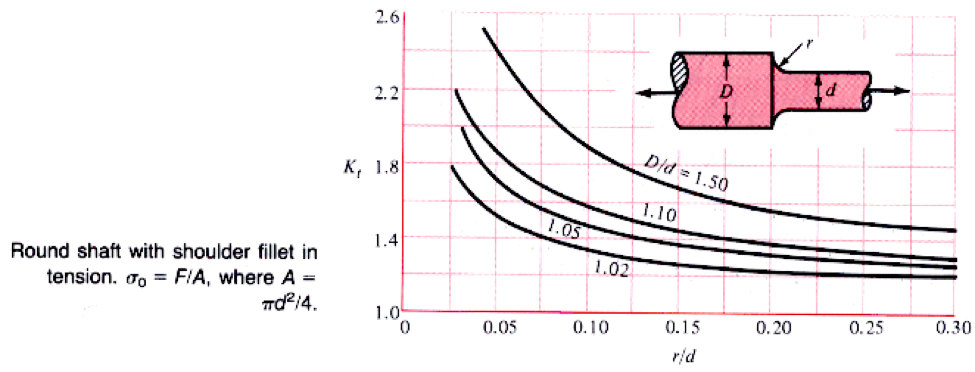
Figura 1. Factor de concentración en eje cilíndrico con filete de hombro bajo carga a tensión (significado de D, d, r). Tomado de: http://classes.mst.edu/civeng110/concepts/06/concentration/index.html
Los experimentos numéricos se realizan para verificar que la herramienta de simulación es capaz de reproducir la concentración de esfuerzo, siempre y cuando la malla utilizada en los puntos de gradientes de esfuerzos más altos (i.e. las mayores variaciones del valor del esfuerzo en el espacio) sea lo suficientemente pequeña como para capturar estos fenómenos.
Tres proporciones geométricas, correspondientes a tres relaciones de aspecto diferentes, fueron consideradas. Para cada geometría se escogieron cuatro tamaños de malla diferentes de tal forma que se realizaron un total de doce simulaciones numéricas. El diámetro mayor D es 0.02 m, la relación D/d es 1.5, y el radio del hombro depende de la razón de aspecto r / d utilizado (0.15, 0.20, 0.24). La cara plana del lado del diámetro mayor del eje está totalmente restringida (i.e. se impone desplazamiento nulo en las tres direcciones) y la cara plana en el lado de menor diámetro del eje soporta un esfuerzo de tensión axial pura de 100,000 Pa. Las otras superficies tienen un desplazamiento libre. En cuanto a las propiedades del material, el módulo de elasticidad E fue de 205 GPa y la relación de Poisson de 0.28 correspondientes a un acero estructural típico.
Se usó una malla tetraédrica con refinamiento local para densificar la malla alrededor del filete de hombro (ver Figura 2). Esta opción permite disminuir el costo informático (i.e la capacidad del computador y el tiempo del cálculo) porque se obtiene la misma precisión con un número menor de grados de libertad cuando se usa malla fina sólo donde existe un fuerte gradiente del desplazamiento, por ejemplo alrededor del hombro. En las simulaciones se utilizaron elementos finitos tetraédricos lineales.

Figura 2. Mallas usadas para una relación de aspecto r/d = 0.15. De izquierda a derecha el tamaño de la malla es de 5.02e-4 m, 2.51e-4 m, 1.67e-4 m y 8.37e-5 m respectivamente. El tamaño de malla se refiere a la longitud característica del tetraedro más pequeño en la zona del filete.
Un ejemplo de los resultados obtenidos se puede ver en la Figura 3 donde es evidente la fuerte concentración del esfuerzo en la dirección axial en el punto donde cambia la sección transversal del eje cilíndrico.
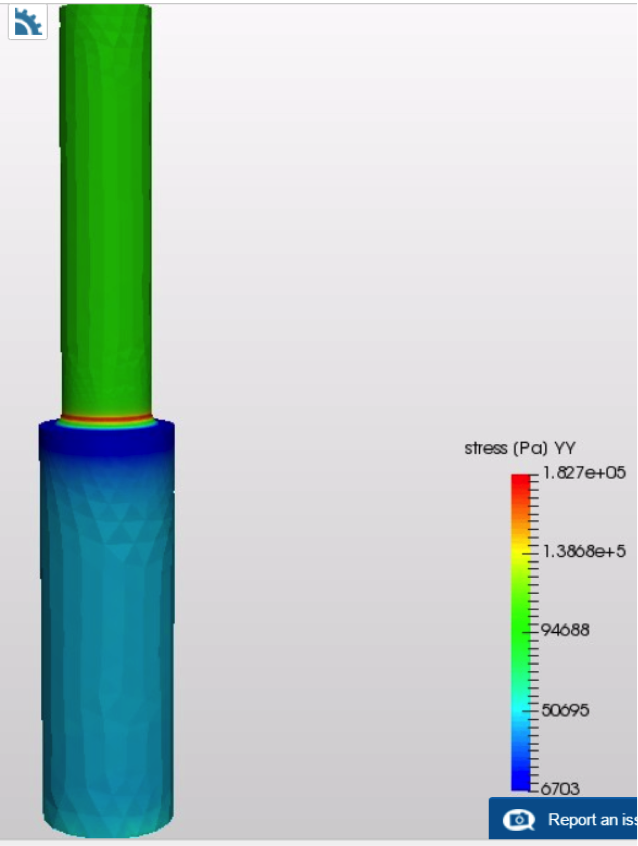
Figura 3. Esfuerzo yy (en la dirección axial) para una razón de aspecto r/d=0.15 y un tamaño de malla de 8.37e-5 m.
Los resultados completos se observan en las tablas 1, 2 y 3 mientras que la figura 4 ilustra la evolución de esfuerzo máximo hacia la verdadera solución como función del número de tetraedros de la malla .
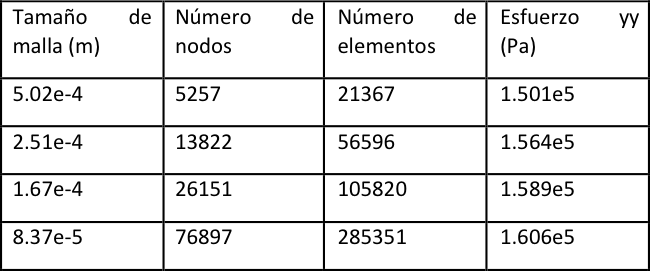
Tabla 1. Resultados de las simulaciones para el caso r/d=0.24.
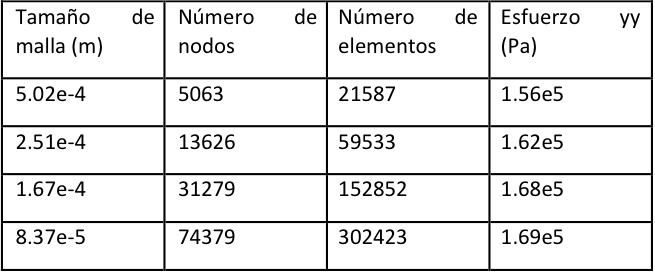
Tabla 2. Resultados de las simulaciones para el caso r/d=0.20.
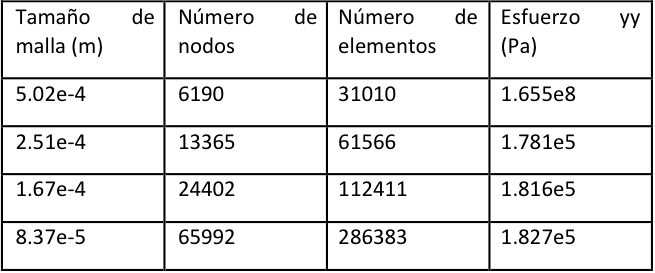
Tabla 3. Resultados de las simulaciones para el caso r/d=0.15.
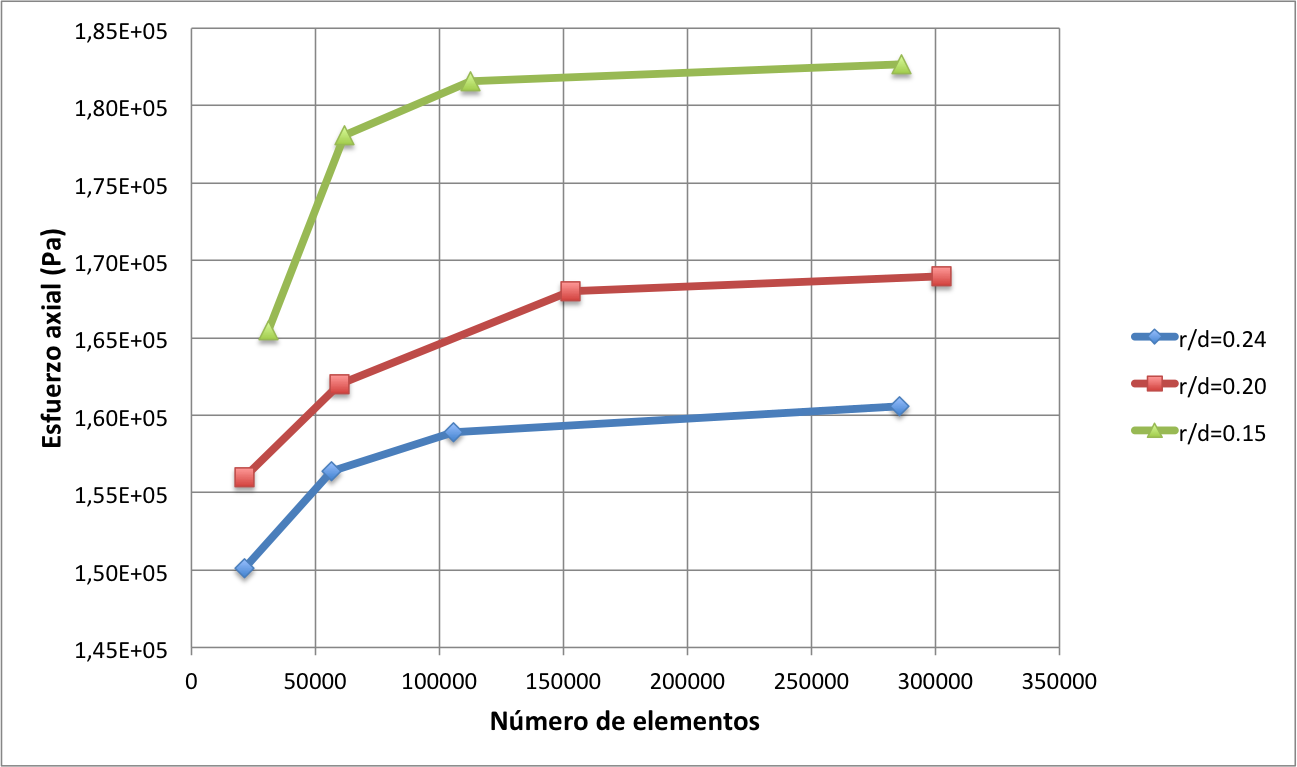
Figura 4. Convergencia de los resultados a la solución analítica en función del número de elementos usados en la simulación. Las soluciones analíticas son 1.6e5 Pa, 1.7e5 Pa y 1.8e5 Pa respectivamente.
En conclusión, los resultados muestran la convergencia del esfuerzo yy (en la dirección axial) con la disminución del tamaño de la malla alrededor del hombro (el lugar donde el gradiente del desplazamiento es más pronunciado) para las tres diferentes razones de aspecto consideradas. El uso de una malla inadecuada en un problema donde la concentración de esfuerzos está presente puede implicar una sobreestimación o subestimación del esfuerzo máximo dentro de una estructura, obteniendo como resultado práctico un costo excesivo en el diseño o, peor, una falla en el servicio de la estructura diseñada. Es indispensable que un ingeniero conocedor de la física del fenómeno analizado use sus criterios profesionales para verificar la pertinencia y la exactitud de los resultados computacionales antes de llevarlos en una aplicación real.
Nota: Estas simulaciones se realizaron en la plataforma en línea SimScale, de la cual Simulmax Engineering es consultor asociado.
